The first two days of the 2048 Infinite Kickstarter have been fantastic! Thanks so much to our (currently) 31 backers who have put us well on our way to making this iOS version of 2048 Infinite – The Circle of Fifths possible. Special thanks to Scott Jon Siegel whose tweet got us an Article at kotaku.com! We ended up having to upgrade our server. Thank you! Technology Tell and Complex Gaming also had kind words to say about 2048 Infinite. Things are going so smoothly that we’ve already decided that we’re going to need some stretch goals.

Stretch goal #1: Upbeat Bird for Android ($700)

We have another game, called Upbeat Bird, that came out only for iPhone back in May. It’s a version of Flappy Bird designed to increase rhythmic accuracy, particularly when playing upbeats. Just like 2048 Infinite, it’s a fun and addictive way to develop a useful musical skill. For another $300 ($700 total) we will be able to get our hands on what we need to put Upbeat Bird out for Android too! This will have a bonus side effect. Rudiment Rock-it will then come out for both Android and iPhone (target date is early August ).

Stretch goal #2: Orchestral Sounds for 2048 Infinite ($1,000)

Caleb (the music guy) wants to design a more complex musical algorithm so the game can play a much larger variety of sounds. Depending on which square the note is formed in, a different instrument will play the pitch. The surrounding harmonic context will play a role in the soundscape as well, resulting in beautiful and lush atmospheric orchestral textures during gameplay. Then Zach will program Caleb’s music into the game.

Thanks so much again for all of the support going into this. We’re super excited to get this iOS version of 2048 Infinite – The Circle of Fifths out into the world!

Click the download icon to help us get this iPhone app accomplished through Kickstarter!

2048 is a sweet game, and the awesome creator of the game, Gabriele Cirulli made it totally free to use and modify. We saw an opportunity to put a musical twist to it and make a music theory game out of it. But we had to modify it a lot to get it to work with 12 different tiles, and then to make it truly infinite. Once we did that, we realized that it was a music game without sound! Caleb (the pro musician of this duo) put more of his music theory skills to work to helped Zach, the programmer, make it sound delicious. Then we made it for Android, and it’s awesome. Zach has completed over 5 circles in one go, and plans to do even better someday. We love it. It’s a great game.

What’s Next: Kickstarter for the iPhone App!

We’re not done with 2048 Infinite – The Circle of Fifths. There must be an iPhone app, but we’re just not quite equipped to make that happen yet. We were going to wait, but why wait when awesome iPhone owning fans are just itching to see it happen asap. With your help through Kickstarter, we’ll get this app finished way sooner than we thought we were going to.

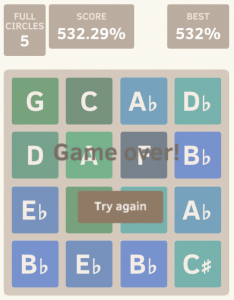
Zach’s high score of 532%

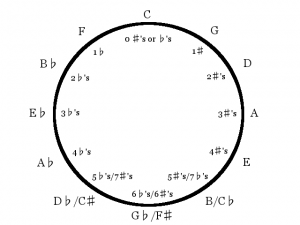
2048 Infinite – The Circle of Fifths is obviously based on the popular game, 2048. However, in using the Circle of Fifths, the game becomes infinite, circular, and almost completely different from the original! With the tiles progressing in a circle, the game becomes mesmerizing. This also means that the score has to be calculated differently. As you play, what was once your high tile will eventually be your low tile. To best reflect your progress in the game, the score is shown in a percentage of full circles completed. If your score is 100%, you’ve gotten one full circle! 200%? Two full circles! I’ve (Zach) gotten past 500% myself. How far can you go?

How do we calculate that score percentage?

Let’s look at an example and I’ll show you how we use all the tiles to calculate a score that reflects the progress in the game. You might have the following tiles on the board: B♭, B♭, A♭, F♯, B, B. Or, listed in a numeric value from counting around the circle of fifths, it would be: 10, 10, 8, 6, 5, 5 (Note: The game actually keeps track of the tiles as numbers like these, and translates them into the appropriate note to display on the screen). One full circle happens when you have made it to the 12th tile. So, with a high tile of 10, the score should be at least 10/12 (83.33%). When we factor in the remaining tiles, the score should be in between 10/12 and 11/12. If we calculate the progress towards a new high tile and add it to 10, we can divide our new number by 12 to get a more accurate score. So let’s use the second highest tile to do that. The progress toward getting a new high tile is the second highest tile divided by the current highest tile. In this case, that is 10/10 (100%). Waitaminute! This leads to a problem: having two of the same highest tiles doesn’t mean you are 100% of the way to a new high tile! Most of the work is done, though, so let’s say that getting two of the same tile is 90% of the work, meaning it should work out to 90% instead of 100%. Our calculation is: 10/10 × 90% = 90%, or 0.9. Add that to 10 to get 10.9 and do 10.9/12 to get a more accurate score: 90.83%.

We can add the third highest tile into the mix, too. Using the second highest tile let us get that 10.9 we used, so let’s use the next tile to add another decimal place onto that and get more precise! The next tile is 8. We can divide 8 by 10, the second highest tile, to get the progress towards getting a new second highest tile. But is that right? To be more accurate, we should calculate it in relation to the current low tile the game is giving. This also means we can just ignore the low tiles on the board because they are not really part of the progress. They’re just handed to you! The low tile at this point is 5, so the calculation is (8-5)/(10-5) × 90% = 0.54. To add it as the next decimal place to the previous number (our 10.9), we do 0.54/10 to get 0.054. 10.9 + 0.054 = 10.954. We can do this with all the remaining tiles to make our number as precise as we can.

That’s a summary of what the game does to calculate the score. Here’s how it looks as the game does everything:

Set of tiles: 10, 10, 8, 6, 5, 5

Progress towards new high tile:
(10−5)÷(10−5)×(9÷10) ⇒ 0.9
+
(8−5)÷(10−5)×(9÷100) ⇒ 0.054
+
(6−5)÷(8−5)×(9÷1000) ⇒ 0.003
= 0.957

Add value of current highest tile:
10.957

Get the score!
10.957 ÷ 12 = 91.31%

After the next move, there is a new high tile. These are the tiles:
F, A♭, F♯, B, B, B
Or, in numbers:
11, 8, 6, 5, 5, 5

Here’s the score calculations for that set of tiles:

Set of tiles: 11, 8, 6, 5, 5, 5

Progress towards new high tile:
(8−5)÷(11−5)×(9÷10) ⇒ 0.45
+
(6−5)÷(8−5)×(9÷100) ⇒ 0.03
= 0.48

Add value of current highest tile:
11.48

Get the score!
11.48 ÷ 12 = 95.67%

2048 Infinite – The Circle of Fifths

Learning the Circle of Fifths deeply is something that can take years to do. When I looked at the circle in high school, I understood very little about it. I knew about how it related to key signatures and the order of flats and sharps. But then there are modes, the fact that it’s a tone row, seeing how it works with symmetrical scales, what it can sound like, understanding how it relates to modulation, transposition, etc. Looking at the circle of fifths can actually get a little overwhelming when you have a deep understanding of it. Learning it exhaustively takes a lot of time and effort. The first step is in understanding where it gets its name and how to draw it out for yourself. The second step is to flat out memorize it.

Why Memorize the Circle of Fifths?

Pathways in the brain that are used often and for a long period of time become fluid mental reflexes. The circle of fifths becomes this for a skilled musician, but only to a point without actually taking the time to study it. Most intermediate (and some advanced) musicians will be a little slow when working with the bottom part of the circle (B, F#/Gb, Db). But learning to think your way around the bottom is crucial both in musical performance and in theoretical understanding. You will be able to read common enharmonic spellings fluently. You will be able to memorize music more quickly by connecting it to the circle. You will understand formal structures and phrasing more coherently. It all starts with having the circle memorized in its entirety. But this can be tedious and frustrating, so we made a game out of it!

The original 2048 has value because it is a game good for the mind in and of itself. But when I played the Dr. Who edition, I quickly realized its potential to help anyone memorize any sequence they wanted to. It has even been applied to pi! Why not reuse the idea to help music students memorize the circle of fifths. And that’s exactly what we did. But we didn’t stop there. This is music, and music should be heard. As you play, you’ll notice how pretty the circle can be. Our plans for the game in the future will include a more complex interactive composition than what we have so far. But for now it is an entertaining and aesthetically palatable way to inherently memorize the circle of fifths. Enjoy!

The simple answer is in a demonstration. Go to a piano. Play a C. Knowing that a flat lowers the affected note by a half-step, play a C flat. Now play a B. Since the B is a half step below the C, C-flat and B are the same note. Any time this happens, it is an enharmonic spelling. 2048 Infinite uses random enharmonic spellings for the three notes that are the most useful to learn to spell enharmonically: B-Cb, F#-Gb, and Db-C#. We have the game switching between these spellings to make you learn them! They are some of the hardest to learn because they are so rarely used. But without them, you will not be able to think your way around the bottom of the circle of fifths.

In the image below, we show all of the most common enharmonic spellings. The beamed notes are enharmonic spellings of each other:

But it gets a little more complicated than that. (This post gets pretty heady at this point. You’ve been warned!) If you are playing an instrument on which you can make small modifications to your pitch, you should bend the note slightly in the direction that the accidental (the pitch modifier) is already going. This is because different intervals tune differently depending of where they are in the chord. For example, let’s say you are in the key of C and you see a B-flat. Most likely, that note is going to be part of a dominant seven chord (borrowed from the key of F), and your pitch should be very low. Do this, and you’ll be in tune. The degree to which you raise or lower your pitch depends on the harmonic context and really just comes down to listening. This concept is called just intonation. Use it!

And now for the nitty gritty stuff that theoreticians and composers like to argue about. The fights I’ve seen are really quite amusing. Is a C-flat equal to a B? Theoreticians (who tend to be more traditional) would say no. Composers (this one, anyway) would say it depends on the time period on harmonic context. Back in the day (1890’s and earlier) nearly everything was tonal. The purpose of equal temperament was for all keys to sound great on instruments that could not be tuned easily (piano, mallet percussion, and others). Composers bent over backwards to make sure they were always in a key. Then Schoenberg happened. When we play atonal music we strictly use equal temperament. Why? Because there’s no key to tune to! Sharps and flats are simply a way to tell the performer what note to play and nothing beyond that. Now, the circle of fifths is technically a tone row. So really it should be interpreted by modern theoreticians as such when no other context is given. The circle of fifths is a very broad tool and should not be limited to the tonal system when using it for analysis.

The circle of fifths is about more than key signatures. It’s a method of understanding sound in general. When teaching the circle of fifths without context, an F-sharp is the same as a G-flat.