Meter is the logical grouping of rhythmic patterns found within music. It is produced when patterns of sounds occur in such a way as to cause the listener to instinctively ascribe a pattern of weak and strong beats to the pulse of the rhythm (Lerdahl and Jackendoff 13). When rhythm generates two or more meters simultaneously, metrical conflict results. This concept is closely related to harmonic dissonance and a clear analogy can be made between the two (Krebs 13). For this reason, this concept will be referred to as metrical dissonance.

When meter is applied to larger time measurements, a hypermetrical structure results. This is a series of strong and weak measures ascribed to the music by the listener due to the larger pattern that is often produced by meter (Caplin 693). When the concept of metrical dissonance is used at the hypermetrical level, dissonance can be heard to be moving more slowly than the primary layer of meter. This idea can be called hypermetrical dissonance (Krebs 55). When applied to progressively higher levels of hypermeter, metrical dissonance can be taken to the extreme of creating dissonance in the formal structure of an entire musical work. When applied to every level of a composition’s hypermeter, the work’s rhythmic components inherently become a fractal. This type of composition can be called a hypermetrical dissonance fractal.

To illustrate this idea, as pure an example as possible of such a composition has been written so that the form can be clearly heard and understood. Since the simplest metrical dissonance possible is two beats played within the same amount of time as three beats, this is the metrical dissonance upon which the fractal will be based. There will be seven hypermetrical levels to the fractal, the highest of which will be a binary form against a ternary form. As each hypermetrical level is added, a different musical element will be used to create the dissonance so that previous levels with not be disturbed by the new level. In order to ensure than no beats are emphasized by a performer’s interpretation or a difference in timbre, very simple synthesizers will be used for this experimental composition.

The first layer of dissonance will be generated by periodic shifts in the timbre of two separate versions of the same synthesizer. One sound will oscillate its timbre twice as the other oscillates three times to create the base metrical dissonance of two against three. This will result in one 6/8 measure (counted in two) against one 3/4 measure so that the listener will be unable to decide if the composite rhythm is in a duple meter or a triple meter. This level of dissonance will remain intact even after more layers have been added.

Example 1: layer 1 notated. Level 1

Layer two will result in a simple hemiola of three bars in duple meter set against two bars in triple meter. To make this apparent, the next logical musical element of pitch change will be used to create each new measure. Both of the sounds will change in pitch at the onset of each new measure according to the meter each sound is representing. The sound oscillating in triple will perform the three measures of duple meter while the sound oscillating in duple will perform the two measures of triple meter. Note that the “sound in triple” is performing the meter that requires three measures to complete the hemiola while the sound in duple is performing the meter that requires two measures to complete the hemiola. This trend will be seen in every level of the fractal, however the terminology will change. The reader should be aware that it is more significant that the sound in triple performs three measures per cycle than that it performs two oscillations per measure. Likewise, it is more significant that the sound in duple performs two measures per cycle than that it performs two oscillations per measure. However, the reader should also be aware that the sounds are indeed changing in pitch every two oscillations regardless of meter.

The “sound in triple” will perform three pitches. In the first measure of the hemiola it will perform a C, in the second measure an E flat, and in the third a G. This will form a broken C minor triad and will set up the tonality to create more possibilities for change in the musical elements so that more layers can be presented. Similarly, the “sound in duple” will change only once, starting on the root and then playing the fifth of the C minor chord.

Example 2: Layer two (bottom) compared with layer one (top). A change in position vertically on the staff represents a change in pitch. Level 2.

Layer three is very similar to layer two since it is still at a level low enough to be grasped as a hemiola. However, at this point the fractal is becoming large enough to where it is useful to think of it as two separate phrase segments being performed simultaneously. This method of thinking will cause the perception of layer four to be a simpler task. The “sound in triple” will perform a three measure phrase segment in 4/4 while the “sound in duple” will perform a two measure phrase segment in 6/4.

Since layer two is sustained by changes in pitch, the next logical musical element to use is harmonic implication. This element has been saved for this level by only using chord tones from a single chord in level two. Each measure will then have a different chord implied by melodic lines from each of the synthesizers. The “sound in triple” will imply a total of three chords (one chord per 4/4 measure) and play a total of six separate tones (maintaining level 2). The “sound in duple” will imply two chords (one chord per 6/4 measure) and a total of four separate tones.

In order for this layer to be successful, two different chords will have to be implied simultaneously. An attempt could be made to maintain harmonic consonance by using only common tones between chords during simultaneous implications. However if only common tones between the chords were used during this harmonic overlap, only the chord which began first would be heard. Harmonic dissonance is unavoidable.
The “sound in triple” will imply a i, iv, V progression while the “sound in duple “will imply a i, V progression. The “sound in triple” could use a simple i, V, i, progression, however this would make a repetition of the cycle difficult to hear since there would be no change in implied harmony from the end of one cycle to the beginning of another. The progression used is more useful for understanding this level. Each chord will be represented only by the root and the third of each chord since the fifth is not necessary to imply harmony.

Example 3: Layer 3 (bottom) compared with levels 1 (top) and 2 (middle). Level 3’s changes in vertical position represents changes in harmony. Event onsets represent new measures. A thick barline represents the start of a new cycle. Level 3

Now that chord progressions are being used, harmonic cadences are possible and will be used to realize the fourth layer. Just as sets of two tones were used to create one unit (chords) in level three, sets of two chords (phrases) will be used to create layer four. Each set of chords will be a i, V progression so that a harmonic cadence is produced. The “sound in triple” will play three cadences to create a three phrase period while the “sound in duple” will play two cadences to create a two phrase period. The chords will continue to change at the same rate so that layer three will not be affected.

The change in the “sound in triple’s” harmonic progression is comparable to the change made to the melodic line when going from layer two to layer three. The element being used to create layer three is harmonic motion; the chords being used do not effect how layer three is heard. Since the “sound in triple” is now oscillating between i and V, layer three’s cycle can be repeated without having three distinct chords. The iv chord is no longer necessary.

Example 4: Starting from the top this example shows layers one, two, three, and four. Each whole note in layer four represents a 4/4 measure and each dotted whole note represents a 6/4 measure. Layer four’s change in vertical position represents a new phrase. Level 4

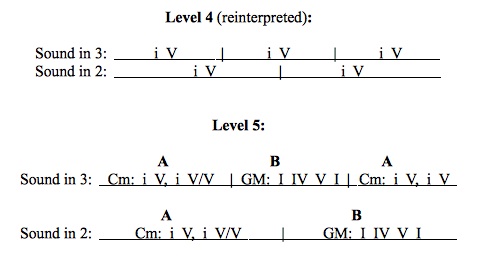
Just as layer three’s phrases formed layer four’s periods, layer four’s periods will form double and triple periods in layer five. The “sound in triple” will perform a triple period while the “sound in duple” performs a double period. Now that formal structure is beginning to come into play, the hypermeter will be increasingly difficult to hear. Layer five then requires two new musical elements to tell the listener where each new period starts with clarity. Now that cadences are being used, modulation can also be employed. However, this is not enough by itself to convince the ear that a new section has begun, so the register the synthesizer is using will change at the start of each new period. These changes will not effect layer four since layer four is driven by cadences alone and all cadences will remain in the same places.

The “sound in triple” will modulate twice by starting in C minor and will use the same register in which it has been. It will then modulate into G Major and shift its register up a full octave at the start of the second period. When it comes to the third period of the triple period, it will perform exactly the same music that it played in the first period. This will make a clear A B A form within the triple period. The “sound in duple” will perform the same music as the “sound in triple” with the exception that the register will shift down an octave instead of up to create a more varied texture. It will also only perform the first two periods and stretch them out over the entire duration of the “sound in triple’s” triple period. This will create a double period against the triple period and make the formal structure of the double period A B.

Since this layer will change the key, distantly related keys will sound simultaneously and create a bitonal texture. At first the entire texture will be in C minor. When the sound in triple modulates initially, G major will be heard in a high voice and C minor in a middle voice. When the sound in duple modulates, G major will be heard in both high and low voices. Lastly, when the sound in triple modulates back to C minor, C minor will be heard in a middle voice while G major will remain in a low voice. The last sonority will be a V in C minor since the sound in duple is modulating back to C minor as well. This strong dominant sonority in the original key leads to a very clear recapitulation in the event of a new cycle.

Example 5: Level 4 has been reinterpreted so that it can be easily compared with level 5. Since formal structures are being referred to, the notation has changed accordingly. Level 5

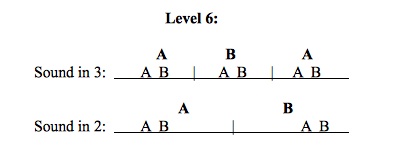
Now that the transition between hemiola and formal structure has been made between layers three, four, and five, the last two layers are much more easily understood both by the mind and the ear. Layer six will take the periods of layer five and use them to create sets of double periods. The sound in triple will perform three double periods while the sound in duple performs two double periods.

Just as in layer five, two changes are needed in order to make the two hypermeters very clear. However, one change occurs naturally; each key area is set against the key area of the other sound in a different way for each double period. At the start of the cycle, both sounds are in C minor. At the start of the “sound in triple’s” second double period C minor is set against G Major. This creates contrast between the sections, especially since the “sound in triple’s” third double period begins in the same way that its first double period begins (both sounds being in C minor at that point). Once again, this creates the desired A B A form for the sound in triple and the A B form for the sound in duple. In addition to this innate characteristic, additional notes have also been added to each sound’s second double period. These additional notes complete the implied harmonies by adding the fifth to each chord.

Example 6: Two double periods against three double periods. Level 6

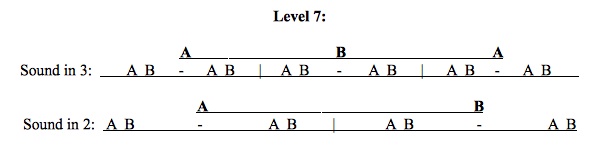
The last layer required to create a short composition using this technique will involve putting double periods into groups of two in order to create sections of a musical composition. This will result in the seventh layer being a binary form against a ternary form. Once again two changes are needed to clearly outline where one section ends and another begins. Just as in layer six, the combinations of sounds (key areas, alternate registers, and additional lines) work together to outline the formal structure of the work naturally. Therefore only one addition is actually needed.

Percussive sounds have also been included in the B sections of the piece to further outline the form. Also, the sounds will be used to subdivide both of the original sound’s timbrel shifts into three so that another layer of the fractal will be produced. This can be thought of as level zero. A highpoint of rhythmic activity will occur when the B section of the “sound in duple” begins and will cause the composition to be a logical artistic gesture.

Example 7: Binary against ternary. Each section is composed to two double periods. Level 7

This pure example of a composition using the hypermetrical dissonance fractal form is strictly for the sake of illustrating that such a piece is possible. It clearly has not yielded music that is consumable by the majority of listeners. However, further exploration of the possibilities and creative variations of the musical elements could very well yield enjoyable music that uses an unexplored formal structure. Creating more interesting melodic material, more complex harmonic progressions, material that unifies the two forms, and elaborating on the rhythms are just a few of many possible ways to create enjoyable sounds using this technique.

Works Cited:

Lerdahl, Fred; Jackendoff, Ray. A Generative Theory of Tonal Music. Cambridge, MA: MIT Press, 1983.

Caplin, William E. Theories of musical rhythm in the eighteenth and nineteenth centuries. The Cambridge History of Western Music Theory. Cambridge, MI: Cambridge University Press, 2002.

Krebs, Harald. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. New York, NY: Oxford University Press, 1999.