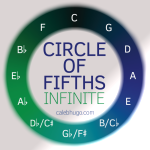
The Circle of Fifths
Things to read before reading about the circle of fifths:
The Circle of Fifths
A fifth is an interval in which the top note is two spaces and two lines away from the bottom note. The easiest way to decide whether or not an interval is a fifth is to count both the lines and spaces starting with the bottom note, and ending with the space or line that the top note is on. If you counted to five, it is a fifth.
When learning about key signatures and the circle of fifths, not just any fifth will work; perfect fifths (P5) must be used. A perfect fifth is a fifth made of seven half-steps. Most fifths that do not use accidentals are perfect. The only exception is when both of the half-step points are inside the interval (this only occurs with the interval between B and F). This makes the interval a half-step smaller than the others (making it six half-steps). An accidental needs to be used to expand it back out to seven half-steps. Look at the the animation on the right. The F can be raised using a sharp, or a flat can be added to the B to keep the interval at 7 half-steps.
When a fifth involves a note with an accidental, all that need be done is to make sure that the other note has the same accidental. If both notes are altered by the same amount and in the same direction, it is still a perfect fifth. The animation to the left demonstrates all of the different fifths possible. Notice how most of the fifths use the same accidental.
To apply fifths to key signatures is quite simple (the hard part is over). There are many ways of thinking about the circle of fifths, and you only need to understand one way in order to begin the learning process. If one method doesn’t make sense, just drop it and move on. It will come to you in time.
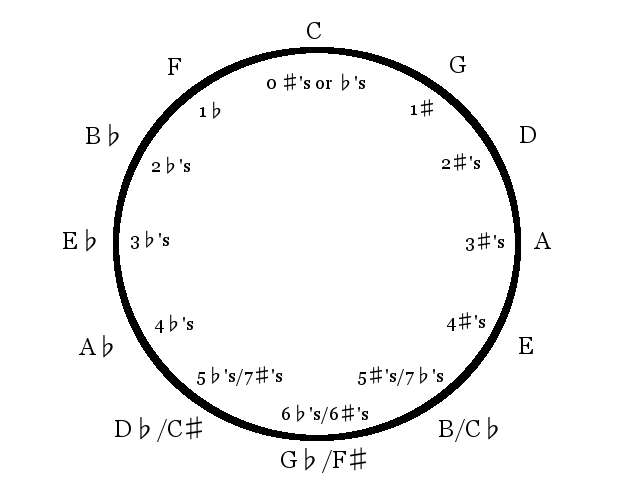The key of C Ionian technically has the a key signature with no sharps or flats (to say it doesn’t have a key signature is not actually true). As we saw in a previous example, the key of G Ionian has one sharp. Notice in example 2-4 that the first interval shows that G is a perfect fifth above C. From this we can see that when the root of a scale goes up a fifth, another sharp is needed in order to correct the pattern necessary to make an Ionian scale. We also, we saw in another example that the key of F Ionian needs one flat in order to correct the pattern. Notice that F is a perfect fifth below C. From this we can see that when the root of a scale goes down a fifth, another flat is needed. Another animation of the circle of fifths (down and to the right) will make this concept clearer.
All this is to say that when the starting pitch of a scale goes up a fifth you add a sharp and when it goes down a fifth you add a flat. The circle of fifths illustrates this concept while also revealing that if you continue to raise or lower your starting pitch by a fifth, you will eventually get back to the key of C.
When going around the circle of fifths to the right, one sharp is added to the key signature for every fifth ascended. When going around the circle of fifths to the left, one flat is added to the key signature for every fifth descended. It can also be thought of this way: for every fifth ascended a flat is subtracted and for every fifth descended, a sharp is subtracted. Adding a sharp and subtracting a flat do the same thing to a key signature. Just pick the method that’s useful to you, and hang on to it.
The image of the circle of fifths should not be memorized, it should be learned. You should understand how fifths build the circle. Once you know how it works, you should have no problem reproducing it (give it a try right now).
Order of Sharps and Flats Using the Circle of Fifths
Now that we know which accidentals to use and how many of them are needed for each Ionian scale, the only problem now is where to put the sharps or flats in the key signature. Once again, the circle of fifths can be used to discover this. Just as we needed to memorize C as our point of departure when learning the Ionian scale, now we need to memorize F-sharp and B-flat to know where to start adding accidentals in key signatures. Here is a way you can remember it: In the first animation (at the top) we learned that a perfect fifth can be formed between B and F by either raising the F or lowering the B—making an F-sharp or a B-flat. This relationship is not arbitrary. In order to correct the pattern and make the Ionian scale that starts on F, we added a B-flat (click for image). Now to discover the B-flat Ionian scale (which is next to the left on the circle and a fifth below F), all we need to do is add an E-flat to the key signature. Since E-flat is a fifth below B-flat, we can see that the next flat we add (when moving to the key of E-flat) is A-flat, then D-flat, G-flat, and C-flat; just follow the circle left. You may also notice that with each new scale the 4th scale degree is being lowered by the new accidental (yet another way to figure it out).
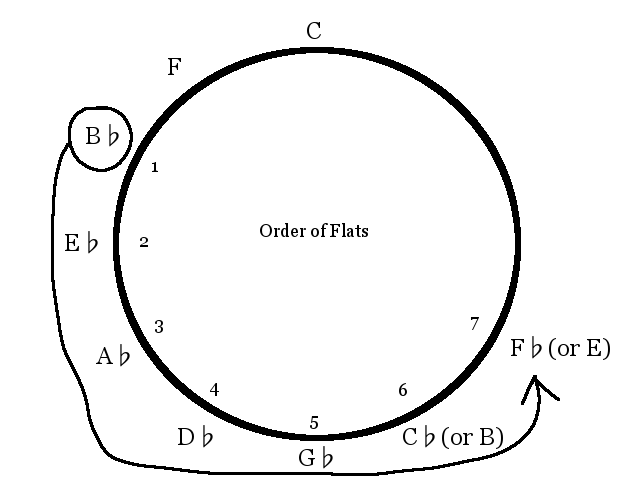
In the same way, to correct the pattern and make the Ionian scale that starts on G, we added an F-sharp (click for image). Now to discover the D Ionian scale (which is next to the right on the circle and a fifth above G), all that need be done is add a C-sharp to the key signature. Since C sharp is a fifth above F-sharp, we find that the next sharp we add is G-sharp, then D-sharp and A-sharp; just follow the circle again, this time starting on F and moving right (see image below). You may also notice that with each new scale the 7th scale degree is being raised by the new accidental (just another way to think about it). Another way to think about the order of sharps is to start with the F-sharp at the bottom of the circle and move clock-wise and respell the pitches. The enharmonic spellings of D-flat, A-flat, E-flat, and B-flat are C-sharp, G-sharp, D-sharp, A-sharp, and E-sharp. Sound familiar? (If I just lost you, forget about the last few sentences.)
Whichever way is easiest for you to learn the circle of fifths, stick with it. There are so many ways to think about this and to get hung up because you don’t understand one method is a mistake. Every one of these methods lead to understanding the circle of fifths. So long as you can draw the circle (without memorizing it) you are good to go. Don’t memorize; learn.