2048 Infinite – The Circle of Fifths

Learning the Circle of Fifths deeply is something that can take years to do. When I looked at the circle in high school, I understood very little about it. I knew about how it related to key signatures and the order of flats and sharps. But then there are modes, the fact that it’s a tone row, seeing how it works with symmetrical scales, what it can sound like, understanding how it relates to modulation, transposition, etc. Looking at the circle of fifths can actually get a little overwhelming when you have a deep understanding of it. Learning it exhaustively takes a lot of time and effort. The first step is in understanding where it gets its name and how to draw it out for yourself. The second step is to flat out memorize it.

Why Memorize the Circle of Fifths?

Pathways in the brain that are used often and for a long period of time become fluid mental reflexes. The circle of fifths becomes this for a skilled musician, but only to a point without actually taking the time to study it. Most intermediate (and some advanced) musicians will be a little slow when working with the bottom part of the circle (B, F#/Gb, Db). But learning to think your way around the bottom is crucial both in musical performance and in theoretical understanding. You will be able to read common enharmonic spellings fluently. You will be able to memorize music more quickly by connecting it to the circle. You will understand formal structures and phrasing more coherently. It all starts with having the circle memorized in its entirety. But this can be tedious and frustrating, so we made a game out of it!

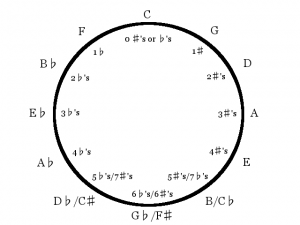The original 2048 has value because it is a game good for the mind in and of itself. But when I played the Dr. Who edition, I quickly realized its potential to help anyone memorize any sequence they wanted to. It has even been applied to pi! Why not reuse the idea to help music students memorize the circle of fifths. And that’s exactly what we did. But we didn’t stop there. This is music, and music should be heard. As you play, you’ll notice how pretty the circle can be. Our plans for the game in the future will include a more complex interactive composition than what we have so far. But for now it is an entertaining and aesthetically palatable way to inherently memorize the circle of fifths. Enjoy!

The simple answer is in a demonstration. Go to a piano. Play a C. Knowing that a flat lowers the affected note by a half-step, play a C flat. Now play a B. Since the B is a half step below the C, C-flat and B are the same note. Any time this happens, it is an enharmonic spelling. 2048 Infinite uses random enharmonic spellings for the three notes that are the most useful to learn to spell enharmonically: B-Cb, F#-Gb, and Db-C#. We have the game switching between these spellings to make you learn them! They are some of the hardest to learn because they are so rarely used. But without them, you will not be able to think your way around the bottom of the circle of fifths.

In the image below, we show all of the most common enharmonic spellings. The beamed notes are enharmonic spellings of each other:

But it gets a little more complicated than that. (This post gets pretty heady at this point. You’ve been warned!) If you are playing an instrument on which you can make small modifications to your pitch, you should bend the note slightly in the direction that the accidental (the pitch modifier) is already going. This is because different intervals tune differently depending of where they are in the chord. For example, let’s say you are in the key of C and you see a B-flat. Most likely, that note is going to be part of a dominant seven chord (borrowed from the key of F), and your pitch should be very low. Do this, and you’ll be in tune. The degree to which you raise or lower your pitch depends on the harmonic context and really just comes down to listening. This concept is called just intonation. Use it!

And now for the nitty gritty stuff that theoreticians and composers like to argue about. The fights I’ve seen are really quite amusing. Is a C-flat equal to a B? Theoreticians (who tend to be more traditional) would say no. Composers (this one, anyway) would say it depends on the time period on harmonic context. Back in the day (1890’s and earlier) nearly everything was tonal. The purpose of equal temperament was for all keys to sound great on instruments that could not be tuned easily (piano, mallet percussion, and others). Composers bent over backwards to make sure they were always in a key. Then Schoenberg happened. When we play atonal music we strictly use equal temperament. Why? Because there’s no key to tune to! Sharps and flats are simply a way to tell the performer what note to play and nothing beyond that. Now, the circle of fifths is technically a tone row. So really it should be interpreted by modern theoreticians as such when no other context is given. The circle of fifths is a very broad tool and should not be limited to the tonal system when using it for analysis.

The circle of fifths is about more than key signatures. It’s a method of understanding sound in general. When teaching the circle of fifths without context, an F-sharp is the same as a G-flat.

The trouble with implementing the sounds in “2048 Infinite – The Circle of Fifths” is that the circle of fifths is a natural tone row. Nothing against tone rows, but it’s not necessarily something people want to hear the entire time they are playing a game. Therefore, it wasn’t a simple matter of having an octave of available sounds to play when the tiles merge. There had to be a logical organization in the orchestration of the chords being formed in order to be palatable to a wide audience. Using some music theory, we found that the solution was to change the bass depending what range of notes the game needed to use.

The way that 2048 Infinite had to be adapted from the original 2048 necessitated that no more than 10 of the 12 different keys be on the board at a time. By the time the player finishes the first circle, there are up to 6 keys displayed. This means that in order for the game to make sounds, it might have to play an F and an F-sharp at the same time without logical tonal harmonic support. Unless, of course, you change the bass note to something the tonicizes the pitch necessary to maintain the impression that a tonal scale is being used.

Using Music Theory to “Set the Mode”

As popular as the Ionian (major) scale is, it’s on the edge of the spectrum when it comes to tension in the church modes. Without a composer asserting his/her total control over it, it can sound sloppy. In the hands of a computer using an algorithm, it can be quite unruly without needlessly complicated logic. The better choice was to tonicize the music using the Aeolian (minor) mode. In 2048 terms, to make the 16 tile the root of the chord.

But why stop there? We then changed that sound to strings to make the music more interesting. But then the bass sounded too exposed, so we let a few other random sounds be strings too.

And that’s how you use music theory to make a tone row tonal.

The trouble with implementing the sounds in “2048 Infinite – The Circle of Fifths” is that the circle of fifths is a natural tone row. Nothing against tone rows, but it’s not necessarily something people want to hear the entire time they are playing a game. Therefore, it wasn’t a simple matter of having an octave of available sounds to play when the tiles merge. There had to be a logical organization in the orchestration of the chords being formed in order to be palatable to a wide audience. Using some music theory, we found that the solution was to change the bass depending what range of notes the game needed to use.

The way that 2048 Infinite had to be adapted from the original 2048 necessitated that no more than 10 of the 12 different keys be on the board at a time. By the time the player finishes the first circle, there are up to 6 keys displayed. This means that in order for the game to make sounds, it might have to play an F and an F-sharp at the same time without logical tonal harmonic support. Unless, of course, you change the bass note to something the tonicizes the pitch necessary to maintain the impression that a tonal scale is being used.

Using Music Theory to “Set the Mode”

As popular as the Ionian (major) scale is, it’s on the edge of the spectrum when it comes to tension in the church modes. Without a composer asserting his/her total control over it, it can sound sloppy. In the hands of a computer using an algorithm, it can be quite unruly without needlessly complicated logic. The better choice was to tonicize the music using the Aeolian (minor) mode. In 2048 terms, to make the 16 tile the root of the chord.

But why stop there? We then changed that sound to strings to make the music more interesting. But then the bass sounded too exposed, so we let a few other random sounds be strings too.

And that’s how you use music theory to make a tone row tonal.